Here we explain how to glass model thermal expansion of optical mounts between lenses in an optical system.
Introduction
Optical systems often operate at different temperatures. OpticStudio provides glass thermal modelling capabilities to model changes in refractive indices and the expansion/contraction of components due to temperature changes. The TCE column in the Lens Data Editor is used to model the thermal effect of the optical mounts between lenses.
The glass thermal expansion of lens mounts
The opto-mechanics or spacer separating 2 lenses (surface 2 in the example below) is represented by an infinitely thin cylinder tube that connects the two lenses. This tube has the same radial extent as the semi-diamater of the surface, so when performing glass thermal analysis, lens semi-diameters should be set equal to the radial height at which the mount contacts the lens. A user-defined aperture may be applied to the lens so that it draws at its real mechanical size: this is what is done in the drawings below.

The glass thermal coefficient of expansion (TCE) of the spacer is specified in the TCE column of the Lens Data Editor (LDE). In the example below, the length of the spacer is larger than the air center thickness, specified in the LDE, due to the lens curvatures and the non-zero radial contact point. The spacer expands or contracts with temperature; both radial and axially. (i.e. it expands in the X, Y and Z axis). The center thickness change is then the result of the change in spacer dimension and lens curvature.
At the nominal system temperature, the semi-diameter of the spacer is the same as the semi-diameter of the contacting glass surfaces (surfaces 2 and 3 in the below example). The semi-diameters of the spacer and lenses will change at different rates if their TCEs are different. The TCE of a glass is specified in the glass catalog. Since the semi-diameter represents the location at which the mount and the lens physically contact at nominal temperature, it should be set equal to the height at which the mount contacts the lens.
Consider the following system.

At the reference/nominal/system temperature, the front part of the spacer is contacting the front lens at semi-diameter of 80 mm and the rear part at 100 mm. Conceptually, you can imagine the spacer being as shown below (colored as light brown in the shaded model below). To create the image below, additional dummy surface was added to change the semi-diameter of the mount before the right lens (see as step change in semi-dimater).

The following animation shows the spacer and the lenses expanding at a different rate (different TCE).

If the TCE of the spacer is set to zero, the length of the spacer does not change with temperature, as shown in the animation below. However, even with zero spacer TCE, the center thickness between the two glasses will change if the radius of any two contacting glass surfaces change with temperature. Observe how in the animation below the center thickness changes while the length of the spacer (highlighted in red) remains fixed.

A numeric example: zero TCE for the spacer
Let’s now consider a numeric example. We’ll start with the system shown on the previous page. We can use the “Make Thermal” tool in the Multi-Configuration Editor to generate a system in which the lenses are at multiple temperatures:
In this case we will choose a single temperature relative to the initial system temperature of 20 degrees C. For simplicity, the temperature chosen will be 120 degrees C (so that DT = 100 degrees C):

The file for this system is named “glass Thermal expansion example zero TCE.zmx”, and the archive (.ZAR) file for this example is located in the Downloads. This system assumes that the TCE value for the spacer between the lenses is zero. As shown on the previous page, the center thickness between the lenses still changes with temperature, since the radii of curvature of each lens changes with temperature. We will calculate the new center thickness value explicitly.
When the TCE value for the spacer is zero, the spacer thickness will remain fixed. The spacer thickness is the distance from the maximum radial aperture of back surface of the first lens to the maximum radial aperture of the front surface of the second lens. This is the case because the radial aperture of the spacer is assumed to be the same as the radial aperture of each of the lens surfaces at the default temperature (20 degrees C). Thus, the radial aperture of the spacer is 80 mm at surface 2 and 100 mm at surface 3.
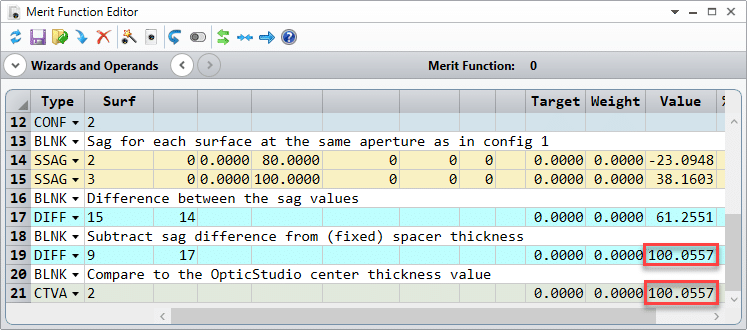
The value for the spacer thickness can be calculated from the sag values of each surface and the center thickness between the surfaces at 20 degrees C (configuration 1). Such a calculation is provided in the first part of the merit function, and the result shows exact agreement with the value for the edge thickness obtained from the ETVA operand:

In configuration 2, the temperature has increased to 120 degrees C, so the radial aperture of each lens surface has also increased. Conversely, the radial aperture of the spacer does not increase, since the TCE value for the spacer is zero. Thus, the spacer thickness is still evaluated using a radial aperture of 80 mm on surface 2 and 100 mm on surface 3. However, since the radii of curvature change with temperature, the sag of each surface at these radial coordinates is different.
Using the new surface sag values, we can calculate what the new center thickness between the lenses must be, in order to maintain the same spacer thickness. This calculation is provided in the second part of the merit function, and the results show exact agreement with the value for the center thickness obtained from the CTVA operand:
A numeric example: finite TCE for the spacer
The calculation for the center thickness between the lenses becomes even more complicated when a finite value for the spacer TCE is used. An example is provided in the file “ glass Thermal expansion example finite TCE.zmx” .
In this example, the TCE value for the spacer is set to 23.6 x 10-6 C-1, which is the standard value for aluminum. Since the TCE value for the spacer is larger than that for the glass (7.1 x 10-6 C-1 for N-BK7), the radial aperture of the spacer will expand by a larger amount than the aperture of each lens surface as the temperature goes from 20 to 120 degrees C.
The first part of the merit function is again dedicated to calculating the spacer thickness at 20 degrees C. In the next part of the merit function, we calculate the multiplication factor that will be used to scale the radial aperture values for the spacer and the lens surfaces:

The values for the new radial apertures (spacer and lenses) are then calculated, along with the sag of the lens surfaces at each aperture value:

We see that the spacer apertures expands to 80.189 mm and 100.236 mm at surfaces 2 and 3, respectively, while the lens apertures expand to 80.057 mm and 100.071 mm at each of these surfaces. In the previous section, we used the spacer apertures to define the spacer thickness, because the spacer apertures were smaller than the lens apertures. In this case the reverse is true, so the lens apertures will be used to define the new spacer thickness.
At the radial aperture to which the spacer expands, the new spacer thickness is:
- Spacer thickness @ spacer apertures = (Spacer thickness @ 20 degrees C)*(1 + TCE*DT)
- Spacer thickness @ spacer apertures = 161.311*(1 + 23.6 x 10-6 C-1*100 degrees C) = 161.692 mm
However, as we just indicated above, the spacer thickness needs to be evaluated at the lens apertures, since these are smaller than the spacer apertures. In this case, the spacer thickness at the lens apertures is given by:
- Spacer thickness @ lens apertures = Spacer thickness @ spacer apertures – (D1 – D2)
- D1 = Sag of surface 2 @ lens aperture – sag of surface 2 @ spacer aperture
- D2 = Sag of surface 3 @ lens aperture – sag of surface 3 @ spacer aperture
From the merit function, we find that:
- D1 = -23.131 mm – (-23.214 mm) = 0.083 mm
- D2 = 38.224 mm – 38.372 mm = -0.148 mm
- D1 – D2 = 0.083 mm – (-0.148 mm) = 0.231 mm
- Spacer thickness @ lens apertures = 161.692 mm – 0.231 mm = 161.461 mm
This is exactly the calculation performed in the third part of the merit function, and the results show exact agreement with the edge thickness value obtained from the ETVA operand (the values are slightly different from my calculations above due to round-off error):

The center thickness value between the lenses is again calculated from the edge thickness and the sag values of the surface, this time at the lens apertures:

Again, exact agreement is found between our calculation and the result obtained in OpticStudio with the CTVA operand.


