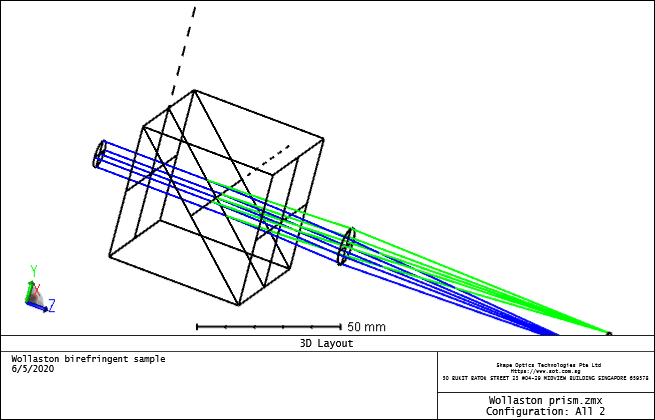
A Wollaston prism splits a broadband input beam into two separately accessible polarization beams with highly pure orthogonal linear polarization. Here is how to design it.
A Wollaston prism is an optical device, invented by William Hyde Wollaston, that manipulates polarized light. It separates light into two separate linearly polarized outgoing beams with orthogonal polarization. The two beams will be polarized according to the optical axis of the two right angle prisms.
The optical axes of each prism in the pair are simultaneously perpendicular to one another and perpendicular to the propagating beam. This results in crystal axis orientation suddenly changing at the interface between the two prisms. The beam component that is S-polarized (relative to the prism hypotenuse) will experience a decrease in refractive index equal to the difference between ordinary and extraordinary refractive indices for Calcite. Light that is P-polarized will experience an equal but opposite change, or an increase of the index from the extraordinary index to the ordinary index. Thus, S- and P- polarized components of the incoming beam will diffract into opposite directions. The final output beams will exit the back port of the polarizer housing with a nominal separation angle of 20 degrees.
Defining the substrate shape
Birefringent In/Out surfaces may be planes, spheres, conic aspheres, or toroids. The default substrate shape is the same as a Standard surface (see “Standard”) defined by the radius of curvature and a conic constant. This standard substrate is called shape 0. The other substrate shape currently supported is shape 1, which is a surface similar to the Toroidal surface except the aspheric coefficients are limited to 10th order and no Zernike terms are supported. The shape number is defined by parameter 6.
Defining the index
To define the ordinary index, OpticStudio uses the glass catalog and glass name in the usual way. For example, to use Calcite, define the surface to be a birefringent “in” type, and enter Calcite for the glass name. OpticStudio uses this name to compute the ordinary index at any defined wavelength. To compute the extraordinary index, OpticStudio appends “-E” to the glass name, and then looks for this material in the glass catalog. For the case of Calcite, OpticStudio searches for “Calcite-E” in the glass catalog, and if found, uses that for the extraordinary index. If not found, an error message is issued. This technique allows definition of any material with any ordinary and any extraordinary index to be defined and used.
Defining the crystal axis for homogeneous materials
For homogeneous materials, the crystal axis orientation is constant throughout the media. The crystal orientation is defined using parameter columns 2, 3, and 4 for the x-, y-, and zdirection cosines of the axis. For example, to define the crystal axis along the x axis, the vector
values are (1, 0, 0). For the axis aligned to the surface vertex normal, which is along the z
axis, the vector is (0, 0, 1).
Determining which ray is traced
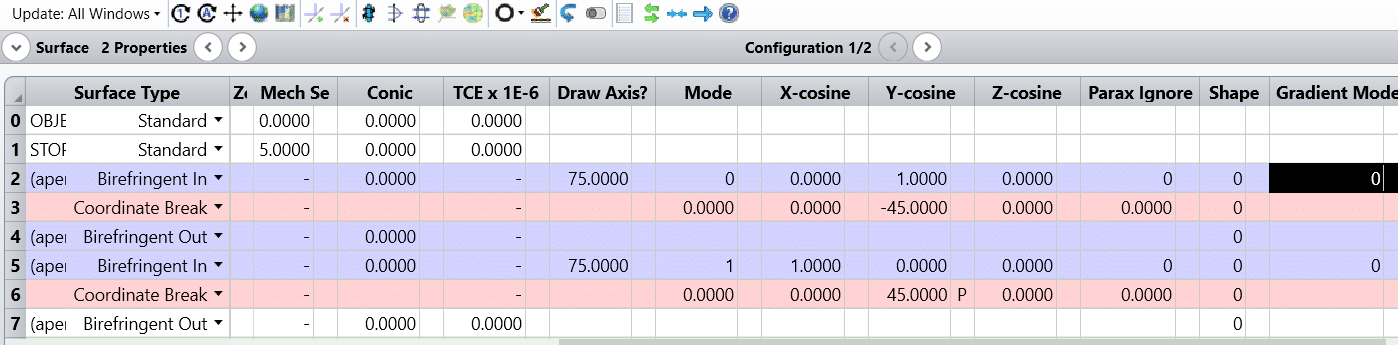
OpticStudio will trace the ordinary ray if the mode is set to 0 or 2. If the mode is set to 1 or
3, the extraordinary ray will be traced. The mode is parameter 1 in the lens data editor.
The setting in sequential mode is as below
It is possible to arrange systems in which an input ray with polarization (1,0) is 100% transmitted, an
input ray with polarization (0,1) is 100% transmitted, but an input ray with (1/sqrt(2), 1/sqrt(2))
is only 50% transmitted. In such circumstances multiple configurations should be used to
fully account for the ordinary and extraordinary ray.
The setting of Non Sequential mode is as below
Reference:
https://en.wikipedia.org/wiki/Wollaston_prism
www.zemax.com, user manual
