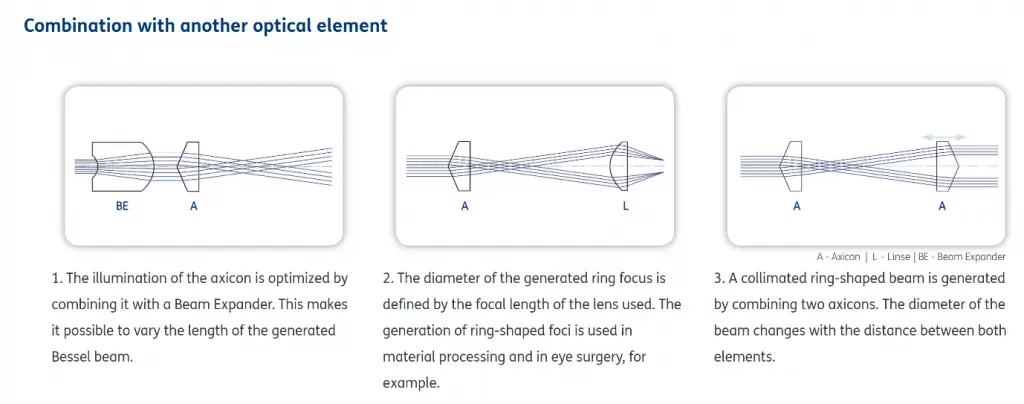
In combination with other lenses, various beam profiles can be generated by Fused Slica Axicon Lens, such as collimated ring beams and variable ring-shaped focal points. How to do it? We share some info here.
An Axicon Lens, is a conical prism defined by its alpha (α) and apex angles, also known as a rotationally symmetric prism, is a lens that features one conical surface and one plano surface.is primarily used

In contrast to aspheric lenses, the shape of an Fused Slica Axicon Lens resembles a cone. The conical shape of the Fused Slica Axicon Lens generates a ring-shaped beam profile. The diameter of the ring beam depends on the axicon angle and decreases as the distance between the axicon and image plane grows. The ring width remains constant.
The Fused Slica Axicon Lens is primarily used in the field of beam shaping and in various laser applications. A particular use is also the generation of non-diffractive Bessel-like beams. An area with almost constant intensity distribution, the length of which is defined by the angle and diameter of the Fused Slica Axicon Lens, is of interest here.
Bessel beams are non-diffractive and ideal for applications in medicine, research, in measuring technology and for adjustments. Specifically, they find use e.g. in optical tweezers and in light fluorescence microscopy. In combination with other axicons or lenses, various beam profiles can be generated, such as collimated ring beams and variable ring-shaped focal points.
Unlike a Gaussian beam which deteriorates over distance, a Bessel beam is non-diffracting, maintaining an unchanged transversal distribution as it propagates. Although a true Bessel beam would require an infinite amount of energy to create, an Axicon Lens generates a close approximation with nearly non-diffracting properties within the Axicon’s depth of focus (DOF).
DOF is a function of the radius of the beam entering the axicon (R), the axicon’s index of refraction (n), and the alpha angle (α):

The simplified equation assumes that the angle of refraction is small and becomes less accurate as α decreases.
Beyond the axicon’s depth of focus, a ring of light is formed. The thickness of the ring (t) remains constant and is equivalent to R:
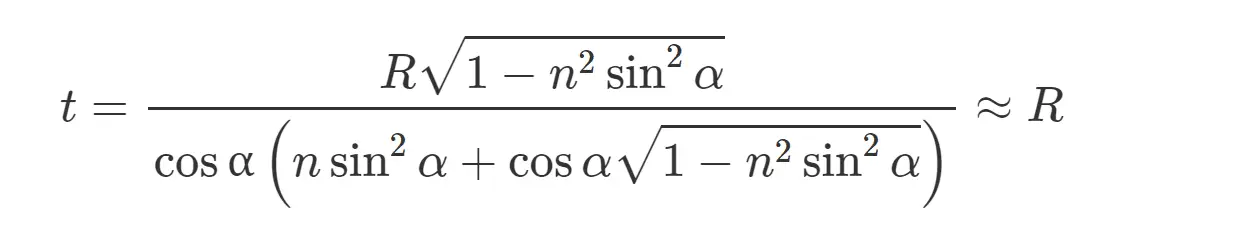
The simplified equation again assumes small angles of refraction. The diameter of the ring is proportional to distance; increasing length from lens output to image (L) will increase the diameter of the ring (dr), and decreasing distance will decrease it.

As mathematically illustrates, the diameter of the ring is approximately related to twice the length, the tangent of the product of the refractive index (n), and the alpha angle (α).
The optical effect in combination with a Beam Expander , a lens or a second Fused Slica Axicon Lens is shown below.


General Specification of Fused Slica Axicon Lens from Shapeoptics
- Apex Round Diameter(S1)<1mm
- Surface Quality(S1, S2): 40/20 scratches-Digs
- Surface Flatness (S2):<1/10 lamda@633nm
- Surface Deviation(RMS)(S1):<0.05um
- Surface Roughness(RMS)(S1):<1nm
- Clear Aperture(S1, S2):>92% of Diameter
- Angular Tolerance: +/-0.02<MOD-DEG>
- Coating Specs(S1,S2): <0.5%@1050nm
- Materail: JGS1, or JGS2 or Corning’s 7980
- Protective chambers:<0.25mmx45<MOD-DEG>


Based on your individual specifications, our optical designers develop the right axicon in terms ofdiameter, center thickness, angle and surface precision. Thanks to the latest production andmeasuring technology, a high level of precision is guaranteed.