How to quickly compute Gaussian beam characteristics, allowing you key into M2 factor and waist size, and displaying beam data as it propagates surface by surface in your optical system, here we will share this tool.

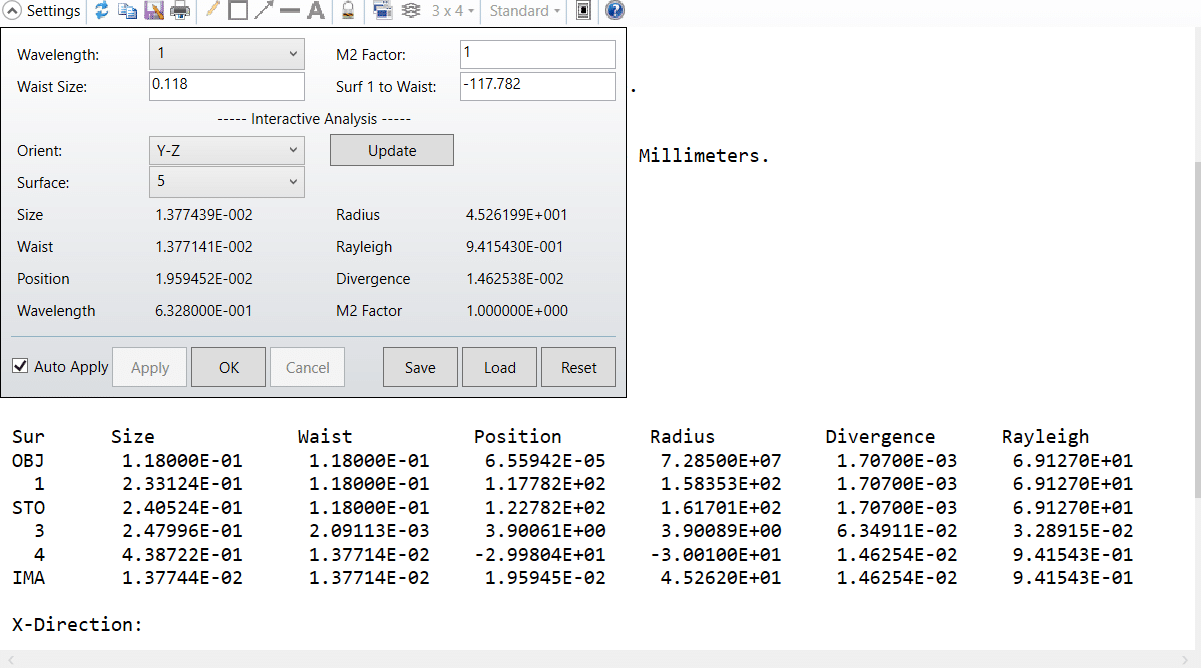
As an laser and optics engineer, we always expect to quickly have the laser beam specs in an system without complicated calculation, here we share a “calculator tool”, paraxial Gaussian beam analysis, which allows you to enter both ideal and mixed mode (M2>1) Gaussian beam and displays beam data as it propagates surface by surface in your optical system. It is an interactive feature that works as a “calculator” that quickly computes Gaussian beam characteristics. This feature computes ideal and mixed mode Gaussian beam data as a given input beam propagates through the lens system. It requires the definition of the initial input embedded beam properties and its M2 value. It propagates this embedded beam through the lens system, and at each surface the beam data, including beam size, beam divergence, and waist locations, is computed and displayed in the output window.
In this article, we will use the same example described in the article: Can We Use “Ray” To Simulate A He-Ne 632nm Laser Source , let’s recap the system parameters.
- Nominal Wavelength = 632.8 nm
- Measured 5 mm from laser output:
- Beam diameter = 0.48 mm
- Measured divergence = 1.7 mrad
Knowing the wavelength and the far field divergence angle, the beam waist is calculated to be 0.118 mm, with a Rayleigh range of 69.7 mm. We will model this system using Paraxial Gaussian beam analysis tool so that the beam spot is the smallest at 30 mm away from the laser output.
The system design and layout is as below:


Here, we’ll look at the Paraxial Gaussian Beam results using 1D Universal Plot to validate the result. This plot shows the computed paraxial Gaussian beam size as a function of the image plane location.

In the plot, you can see the smallest Gaussian beam size 0.014 occurs at a back focal distance around 30 mm, which turns out to be very close to waist size 0.0137mm in the paraxial Gaussian beam calculator. Please take note: The limit is that the calculation of Gaussian beam parameters is based upon paraxial ray data, therefore the results may not be accurate for systems which have large aberrations, or those cannot be described by paraxial optics, such as non-rotationally symmetric systems. This feature also ignores all apertures, and assumes the Gaussian beam propagates well within the apertures of all the lenses in the system.
- The input embedded beam is defined by its Wavelength, Waist Size (radius), and waist location, which is specified using the distance between the beam waist location and surface 1 in the system.
- M2 Factor. The ideal M2 value is unity, but real lasers will always have an M2 value greater than unity.
The design file used in this particle is attached, please download it here. How to computes Gaussian beam characteristics with a “calculator”
Reference Source:
- https://www.zemax.com/
- Zemax Optical Design Program User’s Guide, Zemax Development Corporation
- https://en.wikipedia.org/wiki/Main_Page


