Optical Surface error
  • Lens Fabrication Techniques

PV vs RMS vs Slope Error in Optical Surfaces

Why Surface Error Metrics Matter

When specifying, manufacturing, or testing optical components, understanding surface error metrics is critical. The most commonly used descriptors are:

  • Peak-to-Valley (PV) surface error
  • Root Mean Square (RMS) surface error
  • Slope error

Each metric describes a different physical aspect of surface quality, and no single metric alone is sufficient to fully characterize an optical surface.

This article explains:

  • What each error metric means
  • How they are related
  • Practical engineering rules for converting between them

 

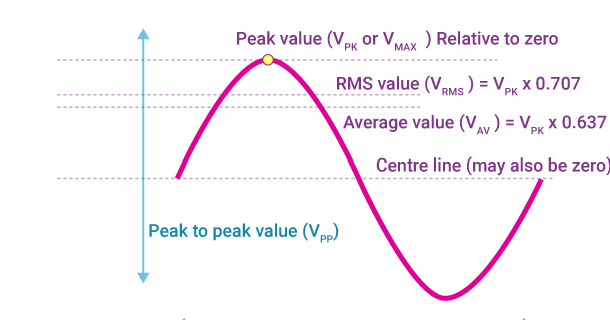
Conversion Between PV and RMS Surface Error

There is no exact mathematical conversion between PV and RMS surface error because:

  • PV measures extremes
  • RMS measures overall distribution

However, for typical, well-polished optical surfaces, an empirical rule of thumb is commonly used:

RMS ≈ PV / 4~5

 

Example

If: PV = 100 nm

Then: RMS ≈ 100/4 = 25nm

Note: This approximation assumes a smooth, low-spatial-frequency surface without isolated defects.

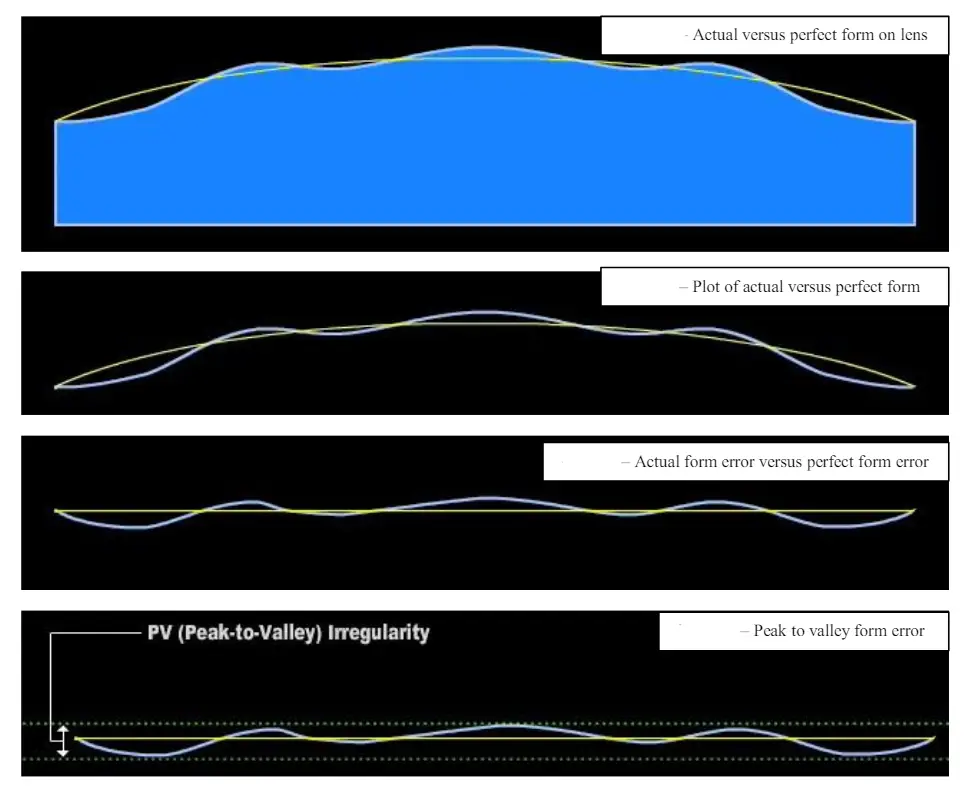
Surface Error

 

Conversion between Surface Error and Slope Error

Slope error is related to the derivative of the surface profile, and therefore depends on spatial frequency.

 

Engineering Approximation

For small angles:

Slope Error (rad) ≈ Surface Error / Spatial Period

Where:

  • Surface Error is in nm
  • Spatial Period is in mm

To convert to microradians:

Slope Error (µrad) ≈ Surface Error (nm) / Spatial Period (mm) × 103

Summary Table

Metric What It Describes Strengths Limitations
PV Maximum deviation Simple, intuitive Over-sensitive to defects
RMS Overall deviation Predicts optical performance Less intuitive
Slope Error Angular deviation Critical for beam direction Depends on spatial frequency

 

Key Takeaways

  • PV and RMS describe different aspects of surface quality
  • RMS is usually more meaningful for imaging performance
  • PV ≈ 4–5 × RMS for typical optical surfaces
  • Slope error depends strongly on spatial frequency
  • Always specify which metric is required in drawings and specifications

 

Measuring Optical Surface Errors

Optical surface errors are commonly measured using:

  • Phase-shifting interferometry
  • Stitching interferometers
  • Deflectometry
  • Autocollimator-based slope measurement