In optical design, it is common to encounter situations where complete dispersion data for a glass material is unavailable. In such cases, Model Glass in OpticStudio provides a practical and reliable way to approximate glass behavior—especially in the visible spectrum.
This article explains:
- What a model glass is
- How to apply the Model Glass Solve in OpticStudio
- The mathematics behind model glass dispersion
- When model glass should—and should not—be used
Using the Model Glass Solve in OpticStudio
A model glass is entered in OpticStudio using a Material Solve in the Lens Data Editor (LDE).
How to Activate the Model Glass Solve
- Open the Lens Data Editor (LDE)
- Locate the Material column for the desired surface
- Click the small cell to the right of the Material field
- Select Model Glass as the solve type
Once activated, OpticStudio internally generates refractive index data based on:
- Refractive index at the d-line (nd)
- Abbe number (Vd)
- Relative partial dispersion behavior
This allows rays to be traced accurately without exposing or requiring full Sellmeier coefficients.

The Mathematics Behind Model Glass
Relative Partial Dispersion
The relative partial dispersion, Px,y between two wavelengths x and y is defined as:

For all glasses in OpticStudio—including model glasses—the reference wavelengths are:
- g-line (Mercury blue): 0.4358343 µm
- F-line (Hydrogen blue): 0.4861327 µm
Therefore, the relative partial dispersion becomes:

Linear Relationship with Abbe Number
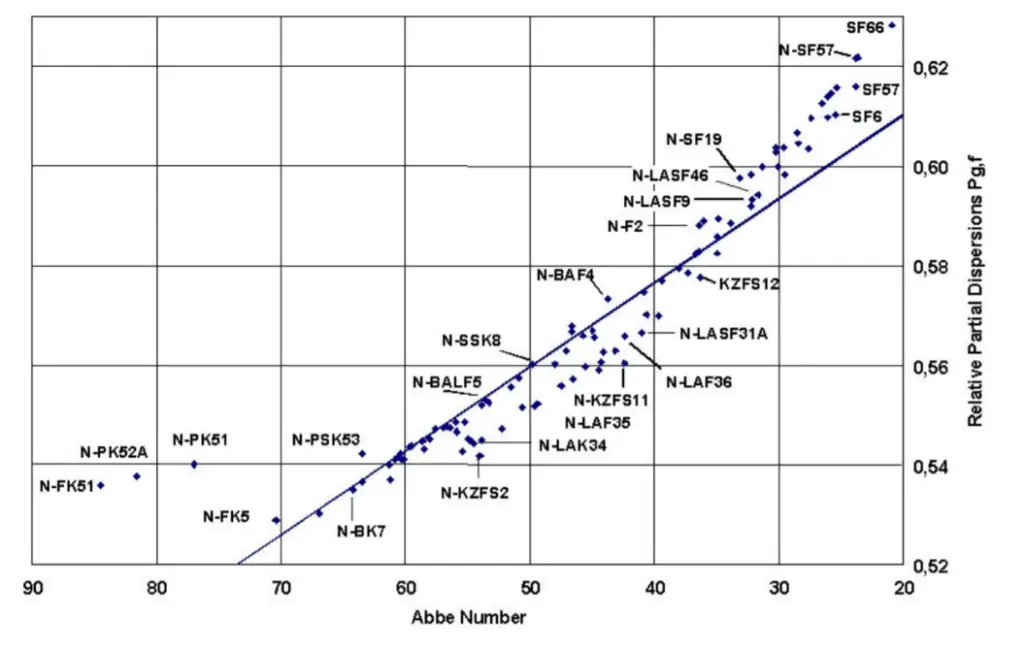
For the majority of optical glasses (often called “normal glasses”), when plotting Relative partial dispersion (P) vs. Abbe number (Vd), the result follows an approximately linear relationship.
OpticStudio leverages this empirical behavior to generate realistic dispersion curves for model glasses.

When to Use Model Glass
Model glass is appropriate when:
- Only limited glass data is available (e.g., nd and Vd only)
- The design operates primarily in the visible wavelength range
- Early-stage feasibility studies or conceptual designs are being performed
- Intellectual property protection requires obscuring exact glass data
In these scenarios, model glass offers surprisingly good accuracy for visible-light imaging systems.
When Not to Use Model Glass
Model glass should not be used when:
- Designing for UV or IR wavelengths
- High-accuracy chromatic performance is required
- Full dispersion data (Sellmeier or tabulated n(λ)) is available
- Glass behavior is critical for thermal, polarization, or laser applications
Outside the visible spectrum, the assumptions behind model glass break down, and errors can become significant.
Best Practice Rule: If accurate dispersion data is available, always use real glass models rather than a model glass.
Model Glass vs. Real Glass Models in OpticStudio
| Aspect | Model Glass | Real Glass |
|---|---|---|
| Required data | nd, Vd only | Full dispersion |
| Visible accuracy | Good | Excellent |
| UV / IR accuracy | Poor | Excellent |
| Design stage | Early / conceptual | Final / production |
| IP protection | Strong | Weak |
Summary
- Model glass is an approximation—not a replacement for real glass data
- It is reliable in the visible spectrum when limited information is available
- It should never replace accurate glass models when full dispersion data exists
- Proper use can speed early design and protect proprietary information
Understanding when and how to apply model glass correctly helps designers avoid subtle but costly chromatic errors later in the design cycle.
References
- Schott AG (April 2005). TIE-29: Refractive Index and Dispersion. In Technical Information – Optics For Devices (Section 2.2). Retrieved from https://wp.optics.arizona.edu/optomech/wp-content/uploads/sites/53/2016/10/tie-29_refractive_index_v2_us.pdf
- Schott – Glass Made of Ideas. 2005 SCHOTT North America. [Online]. September 26, 2005. http://www.us.schott.com/english/index.html
- https://www.zemax.com/